Limits and Continuity

Limit

Suppose f (x) is a real valued function m is a real number. The expression

$$\lim_{x \rightarrow c} f(x)= l$$

This means that f( x ) can be taken very close to l. For example let us consider the function f( x ) in the

$$f(x) = \frac{x^2-1}{x-1}$$

So if you consider x=0.9 then f( 0.9 ) = $\frac{0.9^2 -1}{0.9-1}$ = 1.900. So, if you try some more values like

1. f ( 0.99 ) = 1.990,
2. f ( 0.999 ) = 1.999
3. f ( 1 ) = undefined.
4. f( 1.001 ) = 2.001
5. f( 1.01 ) = 2.010.

$Limit Concept$

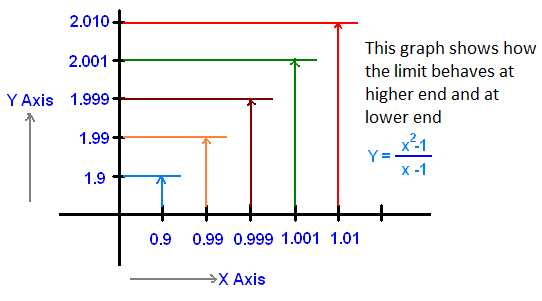
In the above situation, if we take the limit from lower values of x and the other from higher values of x then the function reaches the same value which is approximately equal to 2. so here we can say that the left hand limit is equal to right hand limit and also we say that the limit exists.

1. so f(x) = l = RHS lim exists x- c
2. f(x) = l =LHS lim exits,

Therefore, it is clear that the limit will exists only when right hand side limit is equal to left hand side limit.

Continuity

Function y = f(x) is continuous at point x=b if the following three conditions are satisfied:

1. f(b) is defined ,

2. lim f( x ) exists

Lim f( x ) exists = f(b) is defined ,

Function f is said to be continuous on an interval I if f is continuous at each point x in I. Here is a list of some well-known facts related to continuity:

1. The sum is continuous
2. The difference is continuous
3. The PRODUCT of 2 continuous functions are continuous
4. The quotient of continuous functions is continuous at all points, given that denominator is not zero.
5. The composition of continuous functions is continuous at all points.
6. Any polynomial is continuous for all values of x.
7. Function ex, sinx, cosx are all continuous for all values of x.

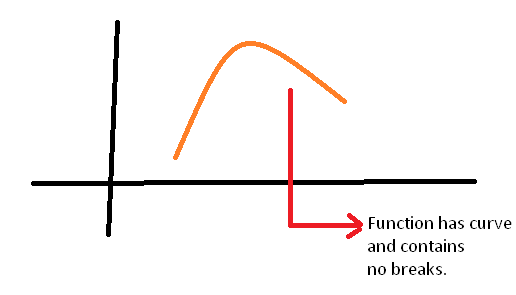
The graph below shows the function which is continuous.

$Continuous Function$

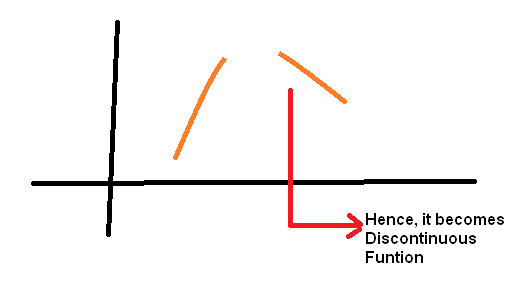
The graph of a discontinuous function

$Discontinuous Function$

Next Chapters

Number Theory	Linear Equation	Set Theory	Math Fractions
Math Functions	Pyramid	Calculus	Cone
Cylinder	Chain Rule	Limits and Continuity	Prime Factorization
Square Roots and Cube Roots	Parabola	Distance Formula	Definite Integrals
Interest	Simple Interest	Compound Interest	Area of Irregular Figures