Area of Irregular Figures

There are various methods of calculating area of irregular figures. These methods give only approximate results. Some of the important methods are given below:

By Simpson's Rule

Divide the base of figure into even number of equal parts and elongate ordinates on each part as shown in the below figure.

Let h = distance between each ordinate

Then, Area = $\frac{h}{3}$ [(y1 + y9) + 2(y3 +y5 + y7) + 4(y2 + y4 + y6 + y8)].

$Area of Irregular Figure$

By Trapezoidal Rule

Divide the base of the figure in equal number of parts and draw ordinates from each of these points as shown below.

If y1, y2..., y6 are the lengths of ordinates and A = distance between each ordinate then

Area = h [$\frac{1}{2}$ (y1 + y6) + y2 + y3 + y4 + y5]

Planimeter

With the help of an instrument known as planimeter, accurate areas can be found very quickly.

Method of counting Squares

Draw the actual irregular diagram on a graph paper to some scale and count the number of squares covered by this diagram, taking those squares greater than one-half as one, and neglecting those having less than one-half of then as covered by the diagram. This gives approximate areas and is used where much accuracy is not desired.

Area of figure = No. of squares x Area of one square.

Area of Trapezium

Area of trapezium = Distance between successive ordinates x Sum of half first and last ordinates, together with all the remaining ordinates.

The Mid-ordinate Method

Divide the base line of the figure into any number of small equal parts and at the centre of each of these parts, draw ordinates as shown below. Calculate the average length of these ordinates and multiply by the length of base line.

This method also gives approximate area.

$Mid-ordinate Method$

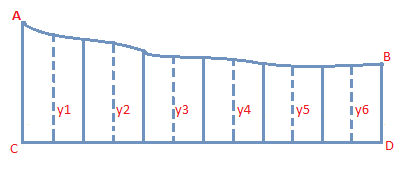
Area = $\frac{(Y_1 + Y_2 + Y_3 + Y_4 + Y_5 + Y_6) \times CD }{6}$

Average of Length of mid ordinates x Length of base line.

Next Chapters

Number Theory	Linear Equation	Set Theory	Math Fractions
Math Functions	Pyramid	Calculus	Cone
Cylinder	Chain Rule	Limits and Continuity	Prime Factorization
Square Roots and Cube Roots	Parabola	Distance Formula	Definite Integrals
Interest	Simple Interest	Compound Interest	Area of Irregular Figures