Set Theory

The study of sets helps in increasing the degree of relations in such a way that it optimizes the bond

between any two ,three or many quantities taken together.

What is a Set?

Set: A well-defined collection of objects is defined as a set.

Example: Set of vowels A= {a, e, i, o, u}

Note: All the sets are denoted by capital letters

Symbols used in sets:

Union: U

Intersection: ∩

Subset: C

If there are two sets given say A and B then the common data found in these two sets is called common data set.

Example A= {a, e, i, o, u} B= {a, i, o}

Then we find the common data set between these two sets namely A ∩ B = {a, i, o}.

The joining of two set elements together is called union of sets

Example: A= {2, 5, 7} B= {a, g, h}

AUB = {a, g, h, 2, 5, 7}

Example A= {1, 5} B= {5}

Then we find the common data set between these two sets namely A ∩ B = {5}.

What is a cardinal number? The number of elements in the given set is called a cardinal number.

Example: A= {1, 2, a, v}

In the above example there are 4 elements in the given set.

Hence we define cardinal number as 4.

Sets Solved Problems

Given A= {1, 2} B= {6, 3}

Find

1. A ∩ B

2. AUB

3. Cardinal number of A and B

If A= {2, 6, 7, 8} B= {2, 6, 3} find A ∩ B

$Set Intersection$

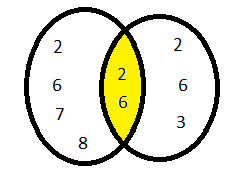
A ∩ B = {2, 6}, so the common elements are shaded in yellow.

In a total of 30 players , 25 play hockey and 10 play Rugby can you predict using set theory that how players are liking to play both.

The formulae is n (A U B) = n (A) + n (B) - n (A ∩ B)

Here n (A U B) = cardinal number of both set A and set B (hockey and rugby)

n (A)= cardinal number of only set A (Hockey only)

n (B) = cardinal number of only set B (Rugby).

And

n (A ∩ B) = cardinal number for both hockey and rugby

30 = 25 +10 - n (A ∩ B) so transfer n (A ∩ B) towards left side we get

n (A ∩ B) = 35-30

= 5

So the number of players who play both is 5.

Next Chapters