Parabola

A parabola is a locus of points in a plane which are equidistant from the line l and the point f not on the line.

$What is Parabola$
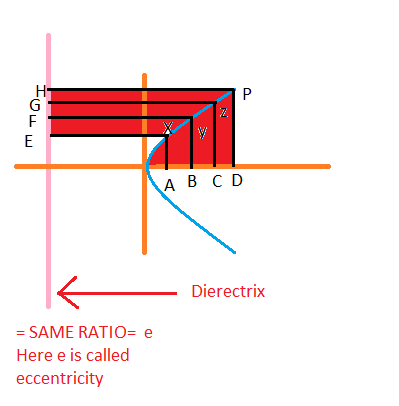
Here f is called the focus and can be refereed as the one of the points A.

If we consider P(x, y) a point on the parabola then we can derive a parabola using the same ratio condition.

We can consider A (a, 0) as the focus point .so then find the distance AP and the distance PH, so by same ratio condition we have $\frac{AP}{PH}$

$\sqrt{(x - a)^2 + y^2)}$ = x + a ------- (1)

(x-a)² + y² = (x + a)² ---------- (2)

x² - 2ax + a² + y² = x² + 2ax + a² ----- (3)

y² = 4ax---- (4).

Equation (4) is the standard equation of the parabola.

Parabola Example

Determine the equations of the parabolas using the following information

The directrix is x = -4 and the focus is (4, 0).

$Parabola Example$

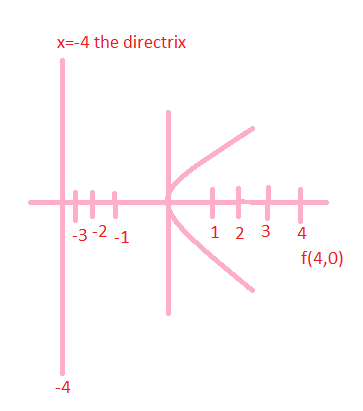
The equation of parabola for the above is given by y² = 4ax. y² = 4(4) x = 16x.

Characteristics of Parabola

A parabola is the graph which is quadratic in nature. It can be in the shape of the letter 'U' or it can be in the shape of the inverted letter of 'U' or C.

There are three main characteristics of a parabola. They are:

Vertex: The point at the apex of a parabola.
X-intercepts: The point at which the parabola touches the x-axis.
Focus: Parabola can be in 8 forms with eight focus.

Based on the above characteristics, there can be six different kinds of parabolas. They are y²= 4ax,

y² = -4ax x² = 4ay x² = -4ay at the vertex as the origin.

Find the equation of the parabola with focus at (-6, 0) and directric x = 6.

Solution: Consider the standard form of parabola y² = 4ax here a = -6

y² = 4 (-6)x = -24x.

Find the equation of the parabola when the length of latest rectum is 24.

Solution: The length of latus rectum = 24

That is 4a = 24

A = $\frac{24}{4}$ = 6

Equation of the parabola

Y² = 4ax

= 4(6)x

= 24x.

Next Chapters

Number Theory	Linear Equation	Set Theory	Math Fractions
Math Functions	Pyramid	Calculus	Cone
Cylinder	Chain Rule	Limits and Continuity	Prime Factorization
Square Roots and Cube Roots	Parabola	Distance Formula	Definite Integrals
Interest	Simple Interest	Compound Interest	Area of Irregular Figures