Distance Formula

The distance between two points is calculated using the formula
$$\sqrt{{(x_{2}-x_{1})^{2}} +(y_{2}-y_{1})^{2}}$$

$What is Distance Formula$

Example1: Find the distance between the points (1, -3) and the point (5, -8)

Solution: The distance between the points A and B is given by the formula
$$\sqrt{{(x_{2}-x_{1})^{2}} +(y_{2}-y_{1})^{2}}$$
Here A= (1, -3) = (x1, y1) and B= (5, -8) = (x2, y2). Now apply this formula
$$\sqrt{{(5- 1)^{2}} +(-8 + 3)^{2}}$$
$$\sqrt{{(4)^{2}} +(-5)^{2}}$$
$$\sqrt{16 + 25}$$
$$\sqrt{41}$$

Example 2: Find the distance between the points (2, -7) and (3, 2)

Solution: The distance between the points A and B is given by the formula
$$\sqrt{{(x_{2}-x_{1})^{2}} +(y_{2}-y_{1})^{2}}$$
Here A= (1, -3) = (x1, y1) and B= (5, -8) = (x2, y2). Now apply this formula
$$\sqrt{{(3- 2)^{2}} +(2 + 7)^{2}}$$
$$\sqrt{{(1)^{2}} +(9)^{2}}$$
$$\sqrt{1+ 81}$$
$$\sqrt{82}$$

Example3: Find the distance between the points (a, b) and (-a, -b).

Solution: The distance between the points A and B is given by the formula
$$\sqrt{{(x_{2}-x_{1})^{2}} +(y_{2}-y_{1})^{2}}$$
Here A= (1, -3) = (x1, y1) and B= (5, -8) = (x2, y2). Now apply this formula
$$\sqrt{{(-a- a)^{2}} +(-b -b)^{2}}$$
$$\sqrt{{(-2a)^{2}} +(-2b)^{2}}$$
$$\sqrt{4a^2 +4b^2}$$
$$2 \sqrt{a^2+b^2}$$

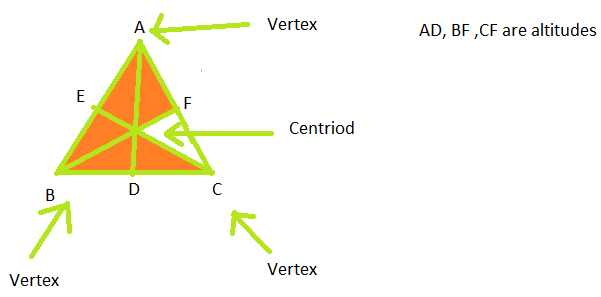
Median : A median is a line segment joining a vertex to a midpoint to the opposite side of the triangle.

Centroid : The intersection of 3 medians of the triangle is called the centroid of the triangle

Centroid Formula

The formula for centroid is given by
$$[ \frac{(x_{1}+x_{2}+x_{3})}{3}, \frac{(y_{1}+y_{2}+y_{3})}{3} ]$$

Examples:

Find the centroid of the triangle with the points (1, 2), (3, 5), (7, 8)

We have the formula
$$[ \frac{(1+3+7)}{3}, \frac{(2+5+8)}{3} ]$$
$$(\frac{11}{3}, \frac{15}{3}) = ((\frac{11}{3}, 5)$$

Find the centroid of the triangle with the points (5, 2), (6, 5), (-7, 8)
We have the formula
$$[ \frac{(5+6-7)}{3}, \frac{(2+5+8)}{3} ]$$
$$(\frac{4}{3}, \frac{15}{3}) = ((\frac{4}{3}, 5)$$

Find the centroid of the triangle with the points (0, 2), (6, 1), (-7, 3)
We have the formula
$$[ \frac{(0+6-7)}{3}, \frac{(2+1+3)}{3} ]$$
$$(\frac{-1}{3}, \frac{7}{3})$$

The above three examples show us how to calculate the centroid.

Ortho Centre: The position where the 3 altitudes of a triangle meet is called the Ortho Centre of the triangle.

The below diagram shows all the above points:

$What is Ortho Centre$

Next Chapters

Number Theory	Linear Equation	Set Theory	Math Fractions
Math Functions	Pyramid	Calculus	Cone
Cylinder	Chain Rule	Limits and Continuity	Prime Factorization
Square Roots and Cube Roots	Parabola	Distance Formula	Definite Integrals
Interest	Simple Interest	Compound Interest	Area of Irregular Figures