Cone

Cone is an object which is hollow, but tapers down to a point at the other end known as the vertex.

A Cone is generated by rotating a right triangle in a clock wise direction or anticlockwise direction.

$How to Make a Cone$

Right circular cone

A Right circular cone is again generated by rotating a right angled triangle rotating clockwise or a clockwise.

Surface Area of a cone

Area of cone has the following specifications

Surface Area of cone = π b l where l² = b² + h²

$Surface Area of a Cone$

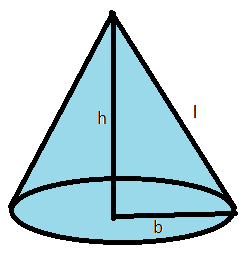
Cone formula

There are three formulas related to cone

1. Surface area of cone = π b l where b is the radius and l is the slant height.
2. Volume of cone = $\frac{1}{3}$ π b² h. where h is the height of the cone.
3. Base area of cone = π b².

Volume of a cone

Volume of cone = $\frac{1}{3}$ π b² h. where h is the height of the cone.

Problems on volume of a cone

1. Find the surface Area of the cone whose base radius is 3cm and height is 4 cm.

Answer: Surface area of cone is given by π b l where b is base radius and l is the slant height.
l² = b² + h²
= 3² + 4²
= 9+16
= 25
l = √25
l=5 cm
Surface Area of the cone = π b l = $\frac{22}{7}$ $\times 3 \times 5$
= 47.14 sq.cm.

2. Find the surface Area of the cone whose base radius is 5cm and height is 12cm.

Answer: Surface area of cone is given by π b l where b is base radius and l is the slant height.
l² = b² + h²
= 5² + 12²
= 25+144
= 169
l = √169
l=13cm
Surface Area of the cone = π b l = $\frac{22}{7}$ $\times 5 \times 13$
= 204.28 sqcm.

3. Find the volume of the cone whose base radius is 6 cm and height is 12 cm.

Answer: The volume of the cone is given by $\frac{1}{3}$ π b² h.
$\frac{1}{3}$ $\times$ $\frac{22}{7}$ $\times$ 6² $\times$ 12 = $\frac{9504}{21}$
= 452.57 cubic cm.

4. Find the volume of the cone whose base radius is 2 cm and height is 21 cm.

Answer: The volume of the cone is given by $\frac{1}{3}$ π b² h.
$\frac{1}{3}$ $\times$ $\frac{22}{7}$ $\times$ 2² $\times$ 21 = $\frac{1848}{21}$
= 616 cubic cm

5. Find the volume of the cone whose base radius is 4cm and height is 35 cm.

Answer: The volume of the cone is given by $\frac{1}{3}$ π b² h.
$\frac{1}{3}$ $\times$ $\frac{22}{7}$ $\times$ 4² $\times$ 35 = $\frac{1760}{7}$
= 251.42cubic cm.

6. Find the surface Area of the cone whose base radius is 5cm and height is 6cm.

Answer: Surface area of cone is given by π b l where b is base radius and l is the slant height.
l² = b² + h²
= 5² + 6²
=25+36
= 71
l = √71
l=8.42cm
Surface Area of the cone = π b l = $\frac{22}{7}$ $\times 3 \times$ 8.42
= 79.44 square cm.

Next Chapters

Number Theory	Linear Equation	Set Theory	Math Fractions
Math Functions	Pyramid	Calculus	Cone
Cylinder	Chain Rule	Limits and Continuity	Prime Factorization
Square Roots and Cube Roots	Parabola	Distance Formula	Definite Integrals
Interest	Simple Interest	Compound Interest	Area of Irregular Figures