Chain Rule

Chain Rule: Chain Rule is differential rule to evaluate the inner functions of the given functions.

Chain Rule Examples

Example y= sin(cosx) , y= log ( tanx). Here cosx is the inner function of sin and tanx is the inner function of log

$Chain Rule Example$

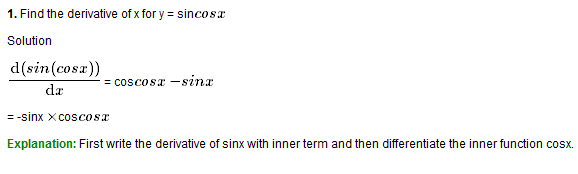
2. Find the derivative of x for y = log(sinx)=$\frac{\mathrm{d} log(sinx)}{\mathrm{d}}$ x $\frac{1}{sinx}$cosx = tanx.

Explanation: First write the derivative of log with inner term and then differentiate the inner function sinx.

3. Find the derivative of y = tan ( secx + cosx)

$\frac{\mathrm{d} tan(secx+cosx)}{\mathrm{d} x}$= $sec^{2}$(secx+cosx)$\times (secxtanx-sinx)

Explanation: First write the derivative of tan with inner term and then differentiate the inner function secx + cosx

For the above example given we can substitute the inner one as u . That is y= sinu so $\frac{\mathrm{d} y}{\mathrm{d} x}$= $\frac{\mathrm{d} y}{\mathrm{d} u}$$\times$$\frac{\mathrm{d} u}{\mathrm{d} x}$.

Chain Rule of Differentiation

1. Find the derivative y=$cos(3x^{4}+8)^2$

Explanation:

Step1: Let $(3x^{4}+8)^2$ =u

So, y= $cosu^2$

we have the formulae $\frac{\mathrm{d} y}{\mathrm{d} x}$=$\frac{\mathrm{d} y}{\mathrm{d} u}$$\times$$\frac{\mathrm{d} u}{\mathrm{d} x}$.

$\frac{\mathrm{d} y}{\mathrm{d} x}$= $\frac{\mathrm{d} cosu}{\mathrm{d} u}$$\times$$\frac{\mathrm{d} (3x^{4}+8)^2 }{\mathrm{d} x}$

step2: sinu$\times$ $2(3x^4)$$\times$ $12x^3$.

Explanation: The derivative of cosu is sinu and the derivative of $u^2$ is 2u and the inner most term is

$x^4$ so the derivative is $4 x^3$.

Next Chapters

Number Theory	Linear Equation	Set Theory	Math Fractions
Math Functions	Pyramid	Calculus	Cone
Cylinder	Chain Rule	Limits and Continuity	Prime Factorization
Square Roots and Cube Roots	Parabola	Distance Formula	Definite Integrals
Interest	Simple Interest	Compound Interest	Area of Irregular Figures