Calculus

Calculus is the study of derivatives. It is based on the rate of change for example if we consider velocity = $\frac{dx}{dt}$. Where, x is the distance, which keeps changing with time.

$What is Derivative$
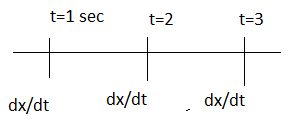
In the above example we see that velocity is different at different time intervals. Hence, we infer this as rate of change of time with respect to distance.

So we always try to say that "A variable is being differentiated with respect to some other variable"

Calculus Formulas

We shall try to put some formulas that is being used regularly.

1. $\frac{d}{dx}$ ( xⁿ) = nx^n-1

2. $\frac{d}{dx}$ (sinx) =cosx

3. $\frac{d}{dx}$(cosx)=-sinx

4. $\frac{d}{dx}$(tanx) =sec² x

5. $\frac{d}{dx}$(cotx) =-cosec²x

6. $\frac{d}{dx}$(secx) = secx tanx

7. $\frac{d}{dx}$(cosecx)= -cosecx cotx

8. $Calculus Formula$
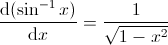
9. $Calculus Formulas$
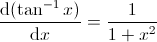
10. $Formula for Calculus$

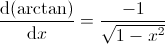
Calculus Problems

Find the derivative of x² + 3 sinx - tanx.

Answer: $\frac{d}{dx}$ ( x²) + 3 $\frac{d}{dx}$( sinx) - $\frac{d}{dx}$(tanx).

We know that the derivative of xⁿ = n x^n-1

so 2x²-1 = 2x

$\frac{d}{dx}$(sinx) = cosx

$\frac{d}{dx}$( tanx) = sec² x.

Answer: 2x + 3cosx -sec² x

Find the derivative of e³x - e ²x + cotx

Answer: $\frac{d}{dx}$ (e³x) -$\frac{d}{dx}$(e²x) + $\frac{d}{dx}$ (cotx)

: 3 e³x - 2 e ²x - cosec² x

The distance travelled by the car is given by the equation X = 3t³-t² find the velocity of the car at the instant t= 1sec

We all know that velocity = $\frac{dx}{dt}$

= $\frac{d}{dt}$ (3t³-t²)

= 3(3t²) - [2t].

= 9 t² -2t

= 9[1] ² -2[1]

= 9-2

= 7m/sec.

The distance travelled by the car is given by the equation X = 3t⁴-t² find the velocity of the car at the instant t= 1sec

We all know that velocity = $\frac{dx}{dt}$

= $\frac{d}{dt}$ (3t⁴-t²)

= 4(3t³) - [2t].

= 12 t² -2t

= 12[1] ² -2[1]

= 12-2

= 10m/sec.

Calculus Problem Solver

The distance travelled by the car is given by the equation X = t³-t⁴ find the velocity of the car at the instant t= 2sec

We all know that velocity = $\frac{dx}{dt}$

= $\frac{d}{dt}$ (t³t⁴)

= 3(t²) - (4t³).

= 3 t² -4t³

= 3[2] ² -4[2] ³

= 12-24

= -12 m/sec. [the vehicle is coming to halt]

The distance travelled by the car is given by the equation X = 3t⁴-t² find the velocity of the car at the instant t= 2sec

We all know that velocity = $\frac{dx}{dt}$

= $\frac{d}{dt}$ (3t⁴-t²)

= 4(3t³) - [2t].

= 12 t² -2t

= 12[2] ² -2[2]

= 48-4

= 44 m/sec.

Next Chapters

Number Theory	Linear Equation	Set Theory	Math Fractions
Math Functions	Pyramid	Calculus	Cone
Cylinder	Chain Rule	Limits and Continuity	Prime Factorization
Square Roots and Cube Roots	Parabola	Distance Formula	Definite Integrals
Interest	Simple Interest	Compound Interest	Area of Irregular Figures